A Brief Review of Learning to Optimize (L2O)

2021-07-21

目标问题

对于一个连续优化问题 $\min_ {\mathbf{x}\in\mathcal{X}}\; f(\mathbf{x})$ ，可以使用迭代的方法获得其（局部）最优解：

\[\mathbf{x}_ {t+1}\leftarrow\mathbf{x}_ {t}+\mathbf{g}(\mathbf{z}_ t;\phi),\tag{1}\]

其中，$\mathbf{z}_ t$ 是第 $t$ 步迭代时可用的信息（例如，已有的迭代点 $\mathbf{x}_ 0,\,\mathbf{x}_ 1,\,\cdots,\,\mathbf{x}_ t$ 以及它们的梯度信息等）；$\mathbf{g}$ 为某个映射函数，一般由 $\phi$ 参数化。Learning to Optimize（L2O）的任务即是在映射函数 $\mathbf{g}$ 的参数空间内学习一个（对于某类问题 $f(\mathbf{x};\theta)$）好的 $\phi$。整体而言，现有的 L2O 方法可分为 model-free 和 model-based 两类^[1]。前者使用通用的神经网络架构实现 $\mathbf{g}$，不参考任何已知的解析优化算法。后者则针对一个现有的解析优化方法，将其整体或部分的迭代更新规则建模为一个可学习的架构，是目前的新方向。

Model-Free L2O

1. LSTM-based L2O

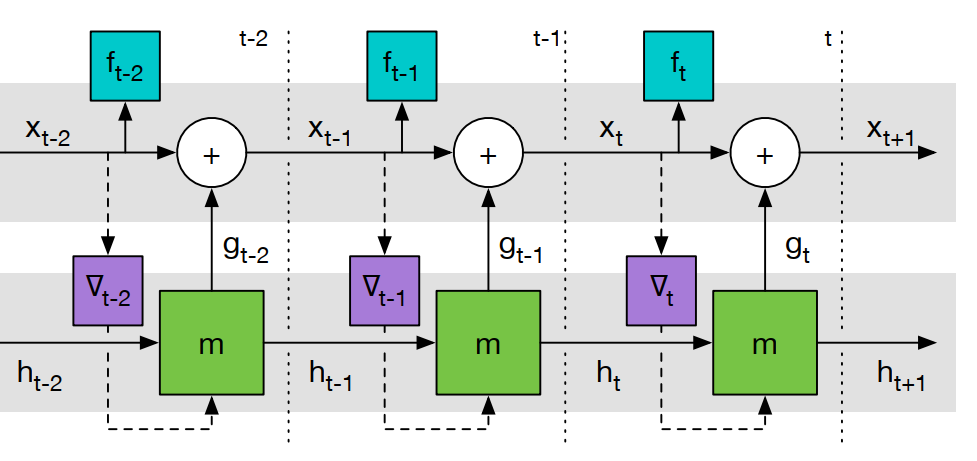
Fig 1. LSTM-based L2O (unrolled form)

优化过程可以看作是迭代更新 $\mathbf{x}$ 的轨迹，故使用循环神经网络（recurrent neural network，RNN）对更新规则建模是自然的选择。图 1 给出了使用一个长短时记忆网络（long short-term memory，LSTM）实现无约束优化问题 $\min_ {\mathbf{x}\in\mathbb{R}^n}\, f(\mathbf{x})$ 的一阶更新的框图，具体而言，即有

\[\mathcal{L}(\phi)=\mathbb{E}_ {f}\left[\sum_ {t=1}^ {T}w_ tf(\mathbf{x}_ t)\right],\;\text{where}\;\;\mathbf{x}_ {t+1}=\mathbf{x}_ t+\mathbf{g}_ t,\;\text{and}\;\begin{bmatrix}\mathbf{g}_ t\\ h_ {t+1} \end{bmatrix}=m\left(\nabla f(\mathbf{x}_ t),\,h_ t,\,\phi\right),\tag{2}\]

其中，$m$ 代表 LSTM，其根据当前时刻的输入（当前点的梯度 $\nabla f(\mathbf{x}_ t)$ ）和网络状态 $h_ {t}$ （包含历史梯度信息），输出更新步 $\mathbf{g}_ t$；$\phi$ 是待学习的网络参数，$\mathcal{L}(\cdot)$ 是损失函数（loss function），T 为LSTM 的展开长度（horizon）。

图 1 的主要问题在于，当优化变量的维度较高时，需要学习的参数过多（标准的 LSTM，一个隐藏单元包含 8 个全连接层）。因此，常见的做法是，采用 Coordinate-wise 的架构^[2]，如图 2 所示，优化变量 $\mathbf{x}_ t$ 的每一个分量的更新单独使用一个 LSTM 实现。同时为了进一步减少网络的参数数量，所有的 LSTM 共享权值，每个优化分量的不同行为通过各自的激活函数实现。

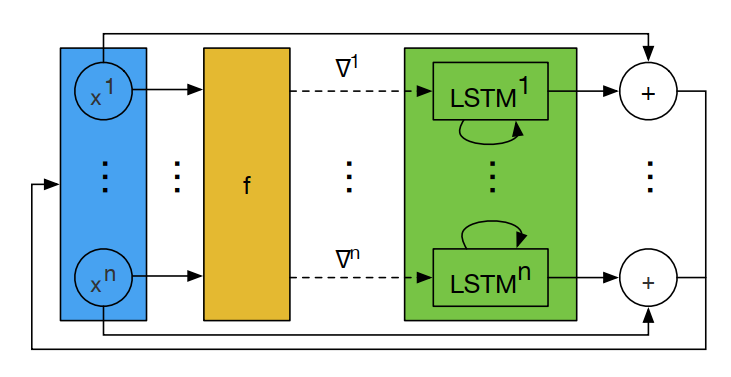
Fig 2. Coordinate-wise LSTM-based L2O (one step)

采用 Coordinate-wise 的架构允许我们使用更小的网络，但其忽略了每个分量之间的联系¹；权值共享在减少参数数量的同时使得优化器对于优化分量的顺序具有不变性，但其忽略了不同分量可能存在的差异性。对于后者，可以根据优化问题的结构，对优化变量进行分组，不同组采用不同的网络参数，组内所有分量则权值共享。对于前者，可以考虑采用 Hierarchical 的网络架构^[3]，如图 3 所示：

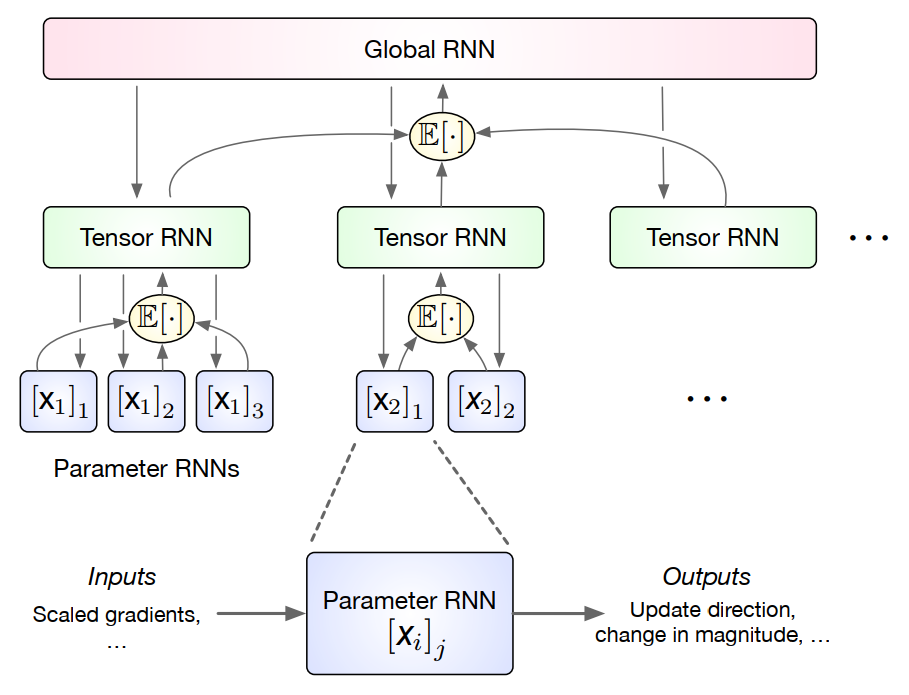
Fig 3. Hierarchical LSTM-based L2O

最底层的 Parameter RNN 仍然实现 Coordinate-wise 的更新；中间层的 Tensor RNN 接受一簇 Parameter RNN（根据问题结构划分）输出值的平均，其输出反过来再加入 Parameter RNN 作为偏差项，用于提取簇内分量的依赖性；最顶层的 Global RNN 接受所有 Tensor RNN 输出值的平均，其输出加入 Tensor RNN 作为偏差项，用于提取簇间的依赖性。通过在底层使用很少量的隐藏元，Hierarchical 架构实现了更低的内存和计算开销。

LSTM-based L2O 面临的一个主要困境是，受限于深层网络训练的困难性，实际中网络的展开长度不能设置过高（10~20 左右）。那么对于一个需要较多步迭代的问题，整个优化轨迹就必须被划分为连续的较短片段，每个片段调用 LSTM 优化器进行优化。这会导致训练好的优化程序在测试时表现出不稳定性并产生低质量的解（截断偏差），如图 4 中黄色曲线所示：

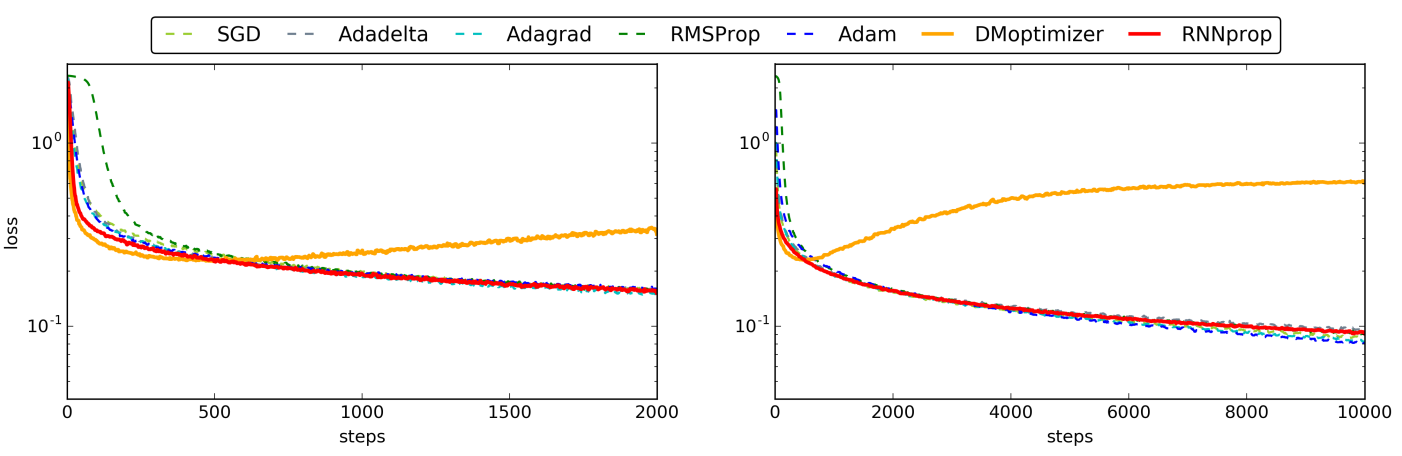
Fig 4. The Behavior of different Optimizers

初步的解决方法是对网络的训练过程进行优化，比如采用渐进式的训练方案^[4]，逐步地增加LSTM网络地展开长度，以缓解截断偏差和梯度消失/爆炸之间的 LSTM-based L2O 困境。

2. RL-based L2O^[5]

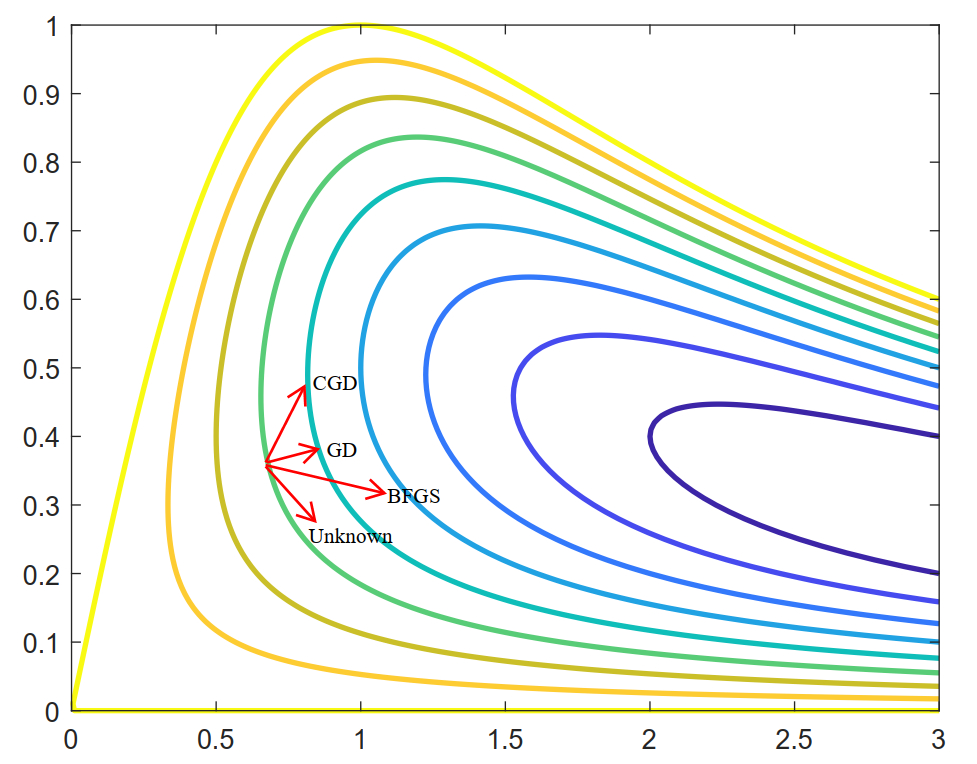
Fig 5. Unconstrained Continuous Optimization

1) 问题

针对某个无约束优化问题 $\min_ {\mathbf{x}\in\mathcal{X}}\; f(\mathbf{x})$ ，学习最优的一阶优化算法，即

\[\mathbf{x}_ {t+1}=\mathbf{x}_ t+\mathbf{F}\left(f(\mathbf{x}_ 1),\cdots,f(\mathbf{x}_ n);\,\nabla f(\mathbf{x}_ 1),\cdots,\nabla f(\mathbf{x}_ n)\right).\tag{3}\]

2) 方法

优化算法的执行可视为马尔可夫决策过程（Markov Decision Process, MDP）中的一个策略的执行，目标就是找到最优的策略（任何一个特定的优化算法，例如梯度下降、共轭梯度法、拟Newton法等，都是一个（确定性）策略；所有的一阶优化算法组成了策略空间）。因此，可以将其建模为一个具有连续动作空间和状态空间的强化学习任务（Policy-based），即

\[\mathbf{F}\left(f(\mathbf{x}_ 1),\cdots,f(\mathbf{x}_ n);\,\nabla f(\mathbf{x}_ 1),\cdots,\nabla f(\mathbf{x}_ n)\right)=\pi(s_ n),\tag{4}\]

其中，状态 $s_ n=\{\mathbf{x}_ n,\nabla f(\mathbf{x}_ n),\cdots,\nabla f(\mathbf{x}_ {n-T+1}),f(\mathbf{x}_ n),\cdots,f(\mathbf{x}_ {n-T+1})\}$，动作空间是所有的一阶更新步（负梯度、共轭梯度、拟 Newton步、Someone Else），惩罚（奖励）函数为 $c(s_ n)=f(\mathbf{x}_ n)$。策略 $\pi$ （的均值）使用两层前馈神经网络参数化：隐藏层包含50个神经元，使用Softplus 激活函数；输出层使用线性激活函数；网络输入状态信息时排除 $\mathbf{x}_ n$​；使用引导策略搜索方法（Guided Policy Search）训练网络。

Model-Based L2O

Model-Free L2O 使用通用的神经网络架构实现优化变量的迭代更新，不参考任何已有的算法，因此具有发现全新算法的可能。其缺点是缺乏理论上的收敛保证和可解释性，同时目前也只适用无约束的简单情形（很难在损失函数中对约束条件进行量化）。与之相对的，Model-Based L2O 选择某个现存的解析算法作为学习的基础构建特定的神经网络架构，网络的特定层、连接关系和激活函数都是对此解析算法的某个操作的模拟。

1. Algorithm Unfolding

Algorithm Unfolding 或 Deep Unfolding 的思想起源是很具有启发性的。考虑 Lasso 问题：

\[\min_ {\mathbf{x}\in\mathbb{R}^ n}\;\frac{1}{2}\lVert\mathbf{y}-\mathbf{W}\mathbf{x}\rVert_ 2^2+\theta\lVert\mathbf{x}\rVert_ 1^ 1,\tag{5}\]

其中，$\theta>0$ 是正则化因子，用于控制解的稀疏性。求解问题 (5) 的经典方法是迭代收缩阈值算法（Iterative Shrinkage and Thresholding Algorithm, ISTA），其属于前向后向分裂（Forward-backward Splitting）方法在 Lasso 问题中的应用，每一步更新包含前向的梯度下降和后向的邻近算子更新，即

\[\mathbf{x}_ {k+1}=\mathcal{S}_ {\lambda}\{\mathbf{x}_ k-\mu\mathbf{W}^ \mathrm{T}(\mathbf{W}\mathbf{x}_ k-\mathbf{y})\}.\tag{6}\]

其中 $\mu$ 为梯度更新的步长，一般选择为 $\frac{1}{\mathrm{eig}_ {\max}(\mathbf{W}\mathbf{W}^\mathrm{T})}$；$\mathcal{S}_ \lambda{x}=\mathrm{sign}(x)(\lvert x\rvert-\lambda)_ +$ 为收缩算子，其来源于 $l_1$ 范数的邻近算子——

\[\mathrm{prox}_ \lambda\{\mathbf{z}\}:\mathbf{z}\rightarrow\arg\min_ {\mathbf{x}}\lVert\mathbf{x}\rVert_ 1+\frac{1}{2\lambda}\lVert\mathbf{x}-\mathbf{y}\rVert_ 2^ 2,\]

收缩因子 $\lambda$ 一般取 $\theta\mu$。现定义矩阵 $\mathbf{W}_ \mathrm{t}\triangleq\mathbf{I}-\mu\mathbf{W}\mathbf{W}^\mathrm{T}$ 和 $\mathbf{W}_ \mathrm{e}\triangleq\mu\mathbf{W}^\mathrm{T}$，则式 (6) 可进一步表示为

\[\mathbf{x}_ {k+1}=\mathcal{S}_ \theta\{\mathbf{W}_ \mathrm{t}\mathbf{x}_ k+\mathbf{W}_ \mathrm{e}\mathbf{y}\},\\ \;\;\;\;\swarrow\quad\;\;\;\searrow\qquad\quad\downarrow\\ \;\mathrm{active}\quad\mathrm{weight}\qquad\mathrm{bias}\tag{7}\]

显然，式 (7) 可以视为神经网络中的一层。因此，ISTA 算法完全可以使用一个神经网络实现，其一次迭代即对应网络中的一层，如图 6 所示——

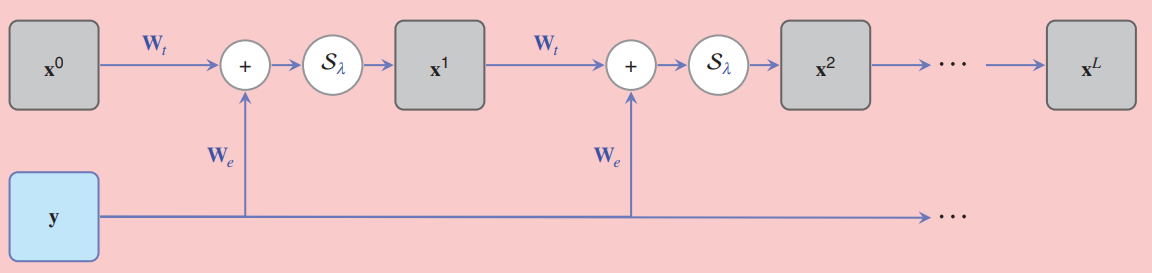
Fig 6. Unfolding ISTA

进一步的，由于引入了可学习的架构，我们可以把矩阵 $\mathbf{W}_ \mathrm{t}$，$\mathbf{W}_ \mathrm{e}$ 以及收缩因子 $\theta$ 都作为网络的参数进行学习优化，以尽可能地加快算法的收敛速度²。对于式 (5) 的无约束问题，网络的损失函数可以直接定义为目标函数以实现无监督训练³。此外，最早提出此方法的文献 [6] 决定每层共享权值，则图 6 可以视为一个 RNN 沿时间线展开的结果，因此得名 Algorithm/Deep Unfolding。在最近的研究中，不同的层使用不同的参数，以更复杂的训练为代价进一步加快算法的收敛速度。此外，除 $l_ 1$ 正则化，其它包括 $l_ 0$，$l_ \infty$ 和更一般的 $l_ p$ 正则化问题，其对应的前向后向分裂算法的展开也陆续地被提出。（事实上，常见的神经网络的激活函数本质上都可以视为是某个函数的邻近算子^[7]：ReLu 函数可以视为是正半区间上示性函数 $\iota_ {[0,+\infty[}(x)$ 的邻近算子，tanh 函数可以视为函数 $\phi(x)=\frac{1}{2}(\iota_ {[-1,+1]}(x)+1)((1+x)\ln(1+x)+(1-x)\ln(1-x)-x^2)$ 的邻近算子。在这个意义上，前向后向分裂算法属于很适合进行展开的一类优化算法。）

2. Learned Operator

作为 Model-based Deep Leaning 的一部分，Algorithm Unfolding 的优势是很显然的。然而，并不是每一个解析算法都可以（直接）展开的。由于神经网络只包含线性操作和简单的标量非线性操作，因此要求待展开的解析算法在一次迭代中每一步都具有简单的闭式形式。如果存在比较复杂的操作（如矩阵求逆、特征分解等），其必须作为额外的数学模块存在于展开的网络中，且要求模块的输出对输入的导数可获得以便使用反向传播训练网络；此时，算法展开的效率可能就大打折扣了。特别地，若存在某一步不具有解析表达，则这个算法可能就根本不适合展开。

对于迭代中包含复杂/非解析操作的优化算法，一种解决方法是将复杂的算子使用神经网络实现。例如，对于问题（5），当考虑比 $l_ 1$ 正则化更复杂的正则化函数时，后向的邻近算子可能没有解析表示，此时就可以使用一个神经网络来实现它。或者，对于带约束优化问题，若其约束条件较为复杂，到其可行域的投影算子不具简单表达，同样使用一个神经网络来实现投影算子^[8][9]，则整体上即可使用投影梯度方法来求解目标问题，如图 7 所示——

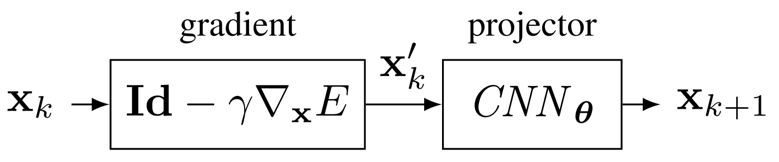
Fig 7. Projected gradient descent using a CNN as the projector

此类方法的思想起源是在深入理解算法中某个算子的物理意义的基础上，使用一个训练好的神经网络代替这个算子。后来进一步提出进行端到端的训练，所以这也可以视为是对 Deep Unfolding 方法的引申。（由于正则项很多情况下都是对解的先验，因此使用神经网络去实现正则函数的邻近算子并进行端到端的训练，本质上也可视为是从数据中学习先验。）

相关文献

[1] Chen T, Chen X, Chen W, et al. Learning to optimize: A primer and a benchmark[J]. arXiv preprint arXiv:2103.12828, 2021.

[2] Andrychowicz M, Denil M, Gomez S, et al. Learning to learn by gradient descent by gradient descent[C]//Advances in neural information processing systems. 2016: 3981-3989.

[3] Wichrowska O, Maheswaranathan N, Hoffman M W, et al. Learned optimizers that scale and generalize[C]//International Conference on Machine Learning. PMLR, 2017: 3751-3760.

[4] Chen T, Zhang W, Jingyang Z, et al. Training stronger baselines for learning to optimize[J]. Advances in Neural Information Processing Systems, 2020, 33.

[5] Li K, Malik J. Learning to optimize[J]. arXiv preprint arXiv:1606.01885, 2016.

[6] Gregor K, LeCun Y. Learning fast approximations of sparse coding[C]//Proceedings of the 27th international conference on international conference on machine learning. 2010: 399-406.

[7] Combettes P L, Pesquet J C. Deep neural network structures solving variational inequalities[J]. Set-Valued and Variational Analysis, 2020: 1-28.

[8] Rick Chang J H, Li C L, Poczos B, et al. One network to solve them all–solving linear inverse problems using deep projection models[C]//Proceedings of the IEEE International Conference on Computer Vision. 2017: 5888-5897.

[9] Gupta H, Jin K H, Nguyen H Q, et al. CNN-based projected gradient descent for consistent CT image reconstruction[J]. IEEE transactions on medical imaging, 2018, 37(6): 1440-1453.