贝叶斯优化（Bayesian Optimization）

2019-08-18

目标问题

贝叶斯优化（Bayesian Optimization）用于解决黑箱无导数全局优化问题（black-box derivative-free global optimization）：

\[\max_ {\mathbf{x}\in\mathcal{X}\subset\mathbb{R}^d}\;f(\mathbf{x}).\tag{1}\]

而与传统的优化问题不同，式（1）具有以下特征：

• 目标函数 $f(\cdot)$ 没有闭式表达（black-box），且导数未知或难以计算（derivative-free），仅可以获得在任意采样点 $\mathbf{x}$ 处的取值 $y=f(\mathbf{x})$ ;
• 对目标函数 $f(\cdot)$ 进行采样/观测（Evaluate）的成本很高，例如，$y=f(\mathbf{x})$ 需要耗费大量资源进行仿真实验获得；
• 不假设函数 $f(\cdot)$ 具有特殊性质，其可能非线性、非凸，可能具有多个局部最优点；
• 优化变量 $\mathbf{x}$ 的维度较低（一般 $d\leq20$ ），约束集 $\mathcal{X}$ 为简单集（超箱、单纯性等）。

由于可解决具有上述性质的优化问题，贝叶斯优化在机器学习的超参数优化任务中应用颇多，尤其是对于深度神经网络和强化学习。

算法思想

由于没有导数信息，黑箱函数的优化需要使用搜索的方法；而如前文所言，对目标函数 $f(\cdot)$ 进行采样的成本高昂。算法的设计目标即是通过尽可能少的采样次数，获得问题（1）的（全局）最优解。在这个意义上，所有求解黑箱函数优化的算法都可以归类为基于模型的序贯优化（sequential optimization），即每步迭代，都使用一个代理函数/模型去近似目标函数 $f(\cdot)$ ，并根据其决定下一步的最优采样位置。

区别于其他方法，贝叶斯优化使用一个统计模型作为函数 $f(\cdot)$ 的代理（surrogate），且在选择新的采样点时使用了贝叶斯方法。具体而言，贝叶斯优化认为目标函数 $f(\mathbf{x})$ 是某个随机过程的一次实现（先验分布 $P(f)$ ），如下图所示

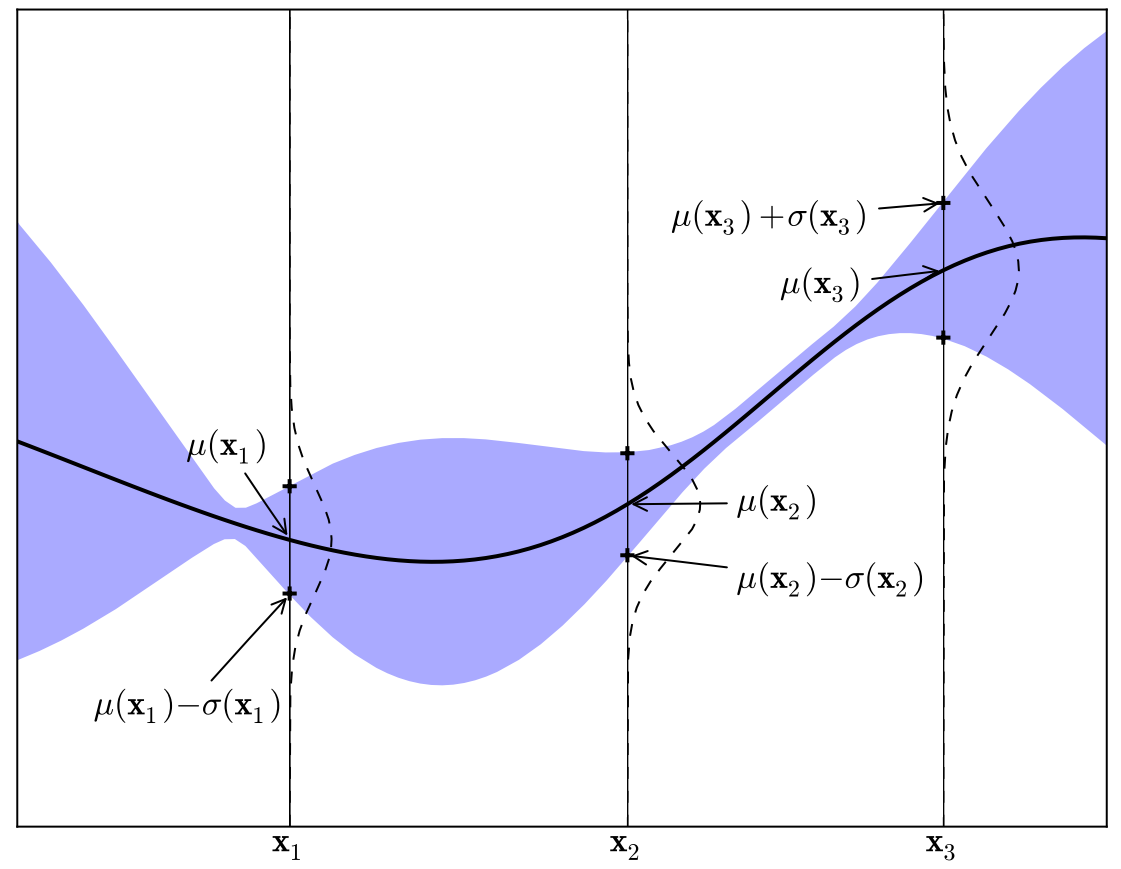
随机过程可视为函数的分布，对于任意的自变量 x（指标），其返回函数 f(x) 取值的一个分布（图中虚线）。或者，可以认为，其返回 f(x) 取值的一个估计值（均值 μ(x)，图中实线），以及此估计的置信程度（方差 σ(x)，图中紫色区域）

设经过前 $t$ 步迭代，已获得样本集 $\mathcal{D}_ {1:t}=\{(\mathbf{x}_ 1,y_ 1),\,\cdots,\,(\mathbf{x}_ t,y_ t)\}$ ；根据贝叶斯理论，我们可以获得目标函数 $f(\mathbf{x})$ 的后验分布：$P(f\vert\mathcal{D}_ {1:t})\propto P(\mathcal{D}_ {1:t}\vert f)P(f)$ 。进而，第 $t+1$ 个采样点可通过最大化某个期望效用函数 $S(\mathbf{x}\vert P(f\vert\mathcal{D}_ {1:t}))$ 进行选取（例如，最大化后验均值 $\mu(\mathbf{x}\vert P(f\vert\mathcal{D}_ {1:t}))$ ），即有

\[\mathbf{x}_ {t+1}\leftarrow\arg\,\max_ {\mathbf{x}}\,S(\mathbf{x}\vert P(f\vert\mathcal{D}_ {1:t})).\tag{2}\]

根据（2）式，在贝叶斯优化中，一般称 $S(\mathbf{x}\vert P(f\vert\mathcal{D}_ {1:t}))$ 为获取函数（acquisition function）。在获得 $\mathbf{x}_ {t+1}$ 处的观测值 $y_ {t+1}=f(\mathbf{x}_ {t+1})$ 之后。重复上述过程，直至达到采样次数上限 $T$ . 最终，算法返回所有观测值中最大的样本点 $f(\mathbf{x}^* )=y_ T^+=\max\{y_ 1,\cdots,y_ t,\cdots,y_ T\}$ 作为优化问题（1）的解。

显然，贝叶斯优化可以视为一个序贯优化方法，其每步迭代，都求解原始优化问题的一个近似/代理问题（即 $\max_{\mathbf{x}}\,S(\mathbf{x}\vert P(f\vert\mathcal{D}_ {1:t}))$ ），最终得到原问题的解。而使用统计模型对函数 $f(\cdot)$ 进行建模，其意义主要有两点：

• 每步迭代，最大化函数 $f(\cdot)$ 取值分布的期望效用，仅追求 “平均” 意义上的最优，（通过设计合适的获取函数）可以较好的平衡 “全局搜索” 和 “局部最优” ，进而使用尽可能少的采样，获得尽可能好的解；
• 由于使用了概率模型，对于存在观测噪声的情况，即 $y_ t=f(\mathbf{x}_ t)+\epsilon_ t$ ，可以很容易地将其包括进来。

算法实现

根据上节的讨论，贝叶斯优化的流程即如上表所示。一个具体的贝叶斯优化算法，主要包括两个要素：1）后验分布 $P(f\vert \mathcal{D}_ {1:t})$ ；2）获取函数 $S(\mathbf{x}\vert P(f\vert\mathcal{D}_ {1:t}))$ 。其中，后验分布 $P(f\vert\mathcal{D}_ {1:t})$ 由先验分布 $P(f)$ 经贝叶斯统计获得，即 $P(f\vert\mathcal{D}_ {1:t})\propto P(\mathcal{D}_ {1:t}\vert f)P(f)$ 。

1. $P(f)$ 的选择

高斯过程几乎是贝叶斯优化中先验分布的标准选择，一方面是由于高斯过程的易解释性和可操作性，另一方面是高斯过程理论上是紧集 $\mathcal{X}\subset\mathbb{R}^d$ 内任意连续函数的统一近似。假设目标函数 $f(\mathbf{x})$ 是高斯过程 $\mathcal{GP}(\mu(\mathbf{x}),\kappa(\mathbf{x},\mathbf{x}’))$ 的一个实现，

\[f(\mathbf{x})\sim\mathcal{GP}(\mu(\mathbf{x}),\kappa(\mathbf{x},\mathbf{x}'),\tag{3}\]

其中 $\mu(\mathbf{x})$ 是高斯过程的均值函数，$\kappa(\mathbf{x},\mathbf{x}’)$ 是高斯过程的核函数，其返回任意样本对 $\mathbf{x}$ 和 $\mathbf{x}’$ 的协方差。设经过前 $t$ 步迭代，获取样本集 $\mathbf{x}_ {1:t}=\{\mathbf{x}_ 1,\cdots,\mathbf{x}_ t\}$ ；对于任意新的样本集 $\mathbf{x}’_ {1:s} = \{\mathbf{x}’_ 1, \cdots, \mathbf{x}’_ s\}$ ，根据式（3），有多维联合正态分布：

\[\left[\begin{array}{c} \mathbf{y}_ {1:t}\\ \mathbf{y}'_ {1:s} \end{array}\right]\sim\mathcal{N}\left(\left[\begin{array}{c} \boldsymbol{\mu}_ {1:t}\\ \boldsymbol{\mu}'_ {1:s} \end{array}\right],\left[\begin{array}{cc} \mathbf{K}_ {xx} & \mathbf{K}_ {xx'}\\ \mathbf{K}_ {x'x} & \mathbf{K}_ {x'x'}\\ \end{array}\right] \right),\tag{4}\]

其中，$\mathbf{y}_ {1:t}=\{y_ 1,\cdots,y_ t\}$ （随机变量 $y=f(\mathbf{x})$ ），$\boldsymbol{\mu}_ {1:t}=[\mu(\mathbf{x}_ 1),\cdots,\mu(\mathbf{x}_ t)]^\mathrm{T}$ ，核矩阵 $\mathbf{K}$ 为对应随机变量的协方差矩阵，

\[\mathbf{K}_ {xx}=\left[\begin{array}{ccc} \kappa(\mathbf{x}_ 1,\mathbf{x}_ 1) & \cdots & \kappa(\mathbf{x}_ 1,\mathbf{x}_ t)\\ \vdots & \ddots & \vdots\\ \kappa(\mathbf{x}_ t,\mathbf{x}_ 1) & \cdots & \kappa(\mathbf{x}_ t,\mathbf{x}_ t) \end{array}\right].\tag{5}\]

现给定观测值 $\mathcal{D}_ {1:t}=\{(\mathbf{x}_ 1,y_ 1),\,\cdots,\,(\mathbf{x}_ t,y_ t)\}$ ，则利用贝叶斯统计，可以得到条件分布 $p(\mathbf{y}’_ {1:s}\vert\mathcal{D}_ {1:t})$ 。特别地，根据正态分布的共轭性，$p(\mathbf{y}’_ {1:s}\vert\mathcal{D}_ {1:t})$ 也是一个多维联合正态分布（亦即函数 $f(\mathbf{x})$ 的后验分布 $P(f\vert\mathcal{D}_ {1:t})$ 仍然是一个高斯过程¹）。具体对于贝叶斯优化而言，由于其是逐点的序贯决策，只需考虑 $s=1$ 的情况（记 $\mathbf{x}’_ 1$ 为 $\mathbf{x}_ {t+1}$ ），此时，我们有条件分布：

\[p(y_ {t+1}\vert\mathcal{D}_ {1:t})=\mathcal{N}\left(\mu_ t(\mathbf{x}_ {t+1}),\,\sigma^2_ t(\mathbf{x}_ {t+1})\right),\tag{6}\]

其均值 $\mu_ t(\mathbf{x}_ {t+1})$ 和方差 $\sigma^2_ {t}(\mathbf{x}_ {t+1})$ 分别为

\[\begin{split} \mu_ t(\mathbf{x}_ {t+1}) &= \mu(\mathbf{x}_ {t+1}) + \mathbf{k}^{\mathrm{T}}\mathbf{K}^{-1}_ {xx}(\mathbf{y}_ {1:t}-\boldsymbol{\mu}_ {1:t}),\\ \sigma^2_ {t}(\mathbf{x}_ {t+1}) &= \kappa(\mathbf{x}_ {t=1},\,\mathbf{x}_ {t+1})-\mathbf{k}^\mathrm{T}\mathbf{K}^{-1}_ {xx}\mathbf{k}, \end{split}\tag{7}\]

其中，$\mathbf{k}=[\kappa(\mathbf{x}_ {t+1},\,\mathbf{x}_ 1),\cdots,\kappa(\mathbf{x}_ {t+1},\,\mathbf{x}_ t)]^\mathrm{T}$ 。式（5）本质上是新采样点 $\mathbf{x}_ {t+1}$ 处目标函数值 $y_ {t+1}=f(\mathbf{x}_ {t+1})$ 的后验预测分布（非参数模型）,其代表了我们当前对于目标函数 $f(\mathbf{x})$ 的认知（简单理解，可以认为后验均值 $\mu_ t(\mathbf{x}_ {t+1})$ 是 $f(\mathbf{x}_ {t+1})$ 的一个点估计，后验方差 $\sigma^2_ {t}(\mathbf{x}_ {t+1})$ 则反映了估计的置信程度）。

显然，对于贝叶斯优化，先验分布 $P(f)$ 的选择是至关重要的。若选择高斯过程，则需要确定的，就是高斯过程的核函数 $\kappa(\mathbf{x},\mathbf{x}’)$ （先验均值 $\mu(\mathbf{x})$ 一般设为常函数，如 $\mu(\mathbf{x})\equiv 0$ ）。主流的选择有两种：

• 平方指数核：$\kappa(\mathbf{x},\,\mathbf{x}’)=\exp\left(-\frac{1}{2\theta}\lVert\mathbf{x}-\mathbf{x}’\rVert^2\right)$
• Marten核：$\kappa(\mathbf{x},\,\mathbf{x}’)=\frac{\alpha}{2^{\zeta-1}\Gamma(\zeta)}\,(2\sqrt{\zeta}\lVert\mathbf{x}-\mathbf{x}’\rVert)^{\zeta}\,H_ {\zeta}(2\sqrt{\zeta}\lVert\mathbf{x}-\mathbf{x}’\rVert)$

它们的基本思想都是，在输入空间 $\mathcal{X}$ 内距离相近的点应当具有更强的相关性（函数的光滑性）。超参 $\theta,\,\alpha$ 和 $\zeta$ 的引入使得模型更为灵活²。

除高斯过程外，概率模型的其他选择还包括 Random Forests，Tree-structured Parzen Estimator 等，但用得都比较少（且或多或少都含有高斯过程/分布的影子）。

2. 获取函数

在贝叶斯优化中，获取函数 $S(\mathbf{x}\vert P(f\vert\mathcal{D}_ {1:t}))$ 的作用是指导每一步的采样位置。一般而言，其本质都是某个效用函数相对于后验预测分布 $p(y\vert\mathcal{D}_ {1:t})$ 的期望。为了”使用尽可能少的采样，获得尽可能好的解“，获取函数需要对所谓的 “exploitation vs exporation” 进行权衡。具体而言，在决定新的采样点时，我们既希望选择有较大把握的样本点（后验均值 $\mu_ t(\mathbf{x}_ {t+1})$ 较大），也希望尝试那些尚未勘探的位置（后验方差 $\sigma^2_ t(\mathbf{x}_ {t+1})$ 较大³。

常见的获取函数有：

1）Probability of Improvement

\[\mathrm{PI}(\mathbf{x})=Pr(f(\mathbf{x})\geq f^+_ t)=\Phi\left(\frac{\mu_ t(\mathbf{x})-f^+_ t}{\sigma_ t(\mathbf{x})}\right)=\Phi(Z),\tag{8}\]

其中，$f^+_ t=\max\{f(\mathbf{x}_ 1),\cdots,f(\mathbf{x}_ t)\}$ ，函数 $\Phi(\cdot)$ 是高斯累积分布函数。本质上，$\mbox{PI}(\mathbf{x})$ 可视为效用函数 $\mathcal{I}(f(\mathbf{x}\geq f^+_ t))$ 相对于后验预测分布 $p(y\vert\mathcal{D}_ {1:t})$ 的期望。显然，式（7）过于偏向 ”exploitation“。改进的方法是引入一个 trade-off 因子，

\[\mathrm{PI}(\mathbf{x})=Pr(f(\mathbf{x})\geq f^+_ t+\xi)=\Phi\left(\frac{\mu_ t(\mathbf{x})-f^+_ t-\xi}{\sigma_ t(\mathbf{x})}\right).\tag{9}\]

若 $\xi$ 很小，算法倾向于”局部最优“；当 $\xi$ 很大，算法倾向于全局搜索。

2）Expected Improvement

在 $\mbox{PI}(\mathbf{x})$ 的基础上，将增益幅度考虑进去即得到 expected improvement 获取函数，

\[\begin{split} \mbox{EI}(\mathbf{x})&=\mathbb{E}\left[\max\{0,\,f(\mathbf{x})-f^+_ t\}\vert\mathcal{D}_ {1:t}\right]\\ &=\begin{cases} (\mu(\mathbf{x})-f^+_ t)\Phi(Z)+\sigma_ t(\mathbf{x})\mathcal{N}(Z), & \mathrm{if}\;\; \sigma_ t(\mathbf{x})>0\\ 0, & \mathrm{if}\;\; \sigma_ t(\mathbf{x})=0 \end{cases} \end{split}\tag{10}\]

显然，使得 $\mbox{EI}(\mathbf{x})$ 增大，要么增大后验均值 $\mu_ t(\mathbf{x}_ {t+1})$ ，要么增大后验方差。获取函 $\mbox{EI}(\mathbf{x})$ 显式地实现了 “exploitation vs exporation” 的权衡。类似于对 $\mbox{PI}(\mathbf{x})$ 的处理，也可引入一个 trade-off 因子增加 $\mbox{EI}(\mathbf{x})$ 的灵活性，

\[\mbox{EI}(\mathbf{x})=\mathbb{E}\left[\max\{0,\,f(\mathbf{x})-f^+_ t-\xi\}\,\vert\,\mathcal{D}_ {1:t}\right].\tag{11}\]

在贝叶斯优化中，$\mbox{EI}(\mathbf{x})$ 是获取函数最常见的选择，且很多时候效果拔群。

3）Upper Confidence Bound

\[\mbox{UCB}(\mathbf{x}) = \mu_ t(\mathbf{x})+\beta_ t\sigma_ t(\mathbf{x}).\tag{12}\]

从形式上看，$\mbox{UCB}(\mathbf{x})$ 很简单，就是后验均值和后验方差的简单加权，直白地实现了 “exploitation vs exporation” 的权衡。但事实上，置信上界函数确实一个理论上很完美的获取函数选择。其思想来源于多臂赌博机（multi-armed bandit）中的 lower confidence bound 算法。通过将贝叶斯优化建模为一个多臂赌博机，从理论上可以证明，使用 $\mbox{UCB}(\mathbf{x})$ 作为获取函数的贝叶斯优化大概率收敛。特别地，参数 $\beta_ t$ 的具体选择也有理论上的指导。

除上述选择外，一些更为复杂的获取函数包括但不限于（Predicative）Entropy Search，Thompson Sampling，和 Knowledge Gradient 等⁴。

总结

最后总结一下贝叶斯方法的优势和劣势。

Pros:

• 理论上较为完备。大部分全局最优算法，尤其是对于黑箱优化，都没有比较好的收敛性证明，而贝叶斯优化具有目前最好的证明；
• 从实际应用来看，就所需要的采样数量而言，贝叶斯优化几乎就是最优的黑箱全局优化算法。

Cons:

• 目前，仅能处理小维度的问题（一般要求 $d\leq 20$ ）；
• 高斯过程核函数的相关参数设置没有（也可能不存在）统一的标准，造成 “用超参去选择超参” 的局面。

相关文献

[1] Shahriari B, Swersky K, Wang Z, et al. Taking the human out of the loop: A review of Bayesian optimization[J]. Proceedings of the IEEE, 2016, 104(1): 148-175.

[2] Frazier P I. A tutorial on Bayesian optimization[J]. arXiv preprint arXiv:1807.02811, 2018.

[3] Snoek J, Larochelle H, Adams R P. Practical bayesian optimization of machine learning algorithms[J]. Advances in neural information processing systems, 2012, 25.