8 位浮点数

2017-11-18

定点数与浮点数

严格上讲，计算机存储的只能是固定位数的整数。对于含有分数部分的数，计算机无法识别 “.” ，目前的处理方式有定点（fixed-point）和浮点（floating-point）两种。

假设现在可用一个字节（8 比特）存储一个数（比如 $5.5_ {(10)}$ ）。对于定点数，顾名思义，即 “.” 始终固定在给定的存储位的同一位置。下图给出了使用（8，4）定点数表示 $5.5_ {(10)}$ 的示意图：

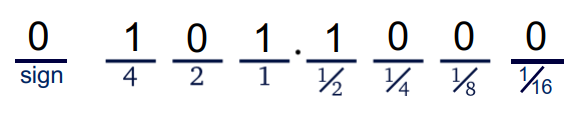
形式上看， “.” 将8个比特位划分为两部分， “.” 左边的位表示整数部分， “.” 右边的位表示分数部分。即在实际存储时，用两个半字节整数表示一个定点数，只不过小数点后的第一位是半位，下一位是四分之一位，下一位是八分之一位，以此类推。定点数的形式简洁，也易于硬件实现，其缺点在于表示范围受限。以8位定点数为例，上图的（8，4）形式可表示的最大正数为 $2^3 = 8_ {(10)}$ ，即便采用（8，1）的形式也只可以表示到 $2^6=64_ {(10)}$ 。大多数程序在计算过程中需要使用范围更广的数字，因此定点数在当今的计算世界并不常用。

浮点数的思想，本质上可以视为2进制的科学计数法。还是以 $5.5_ {(10)}$ 为例，其二进制形式为 $101.1_ {(2)}$ ，转换为科学计数法即为 $1.011_ {(2)}\times 2^{\color{red} 2}$ ；遵循科学计数法的命名，$1.011_ {(2)}$ 称为尾数（mantissa）或有效数，$\color{red} 2$ 称为指数（exponent）。所以，给定存储位数，浮点数格式可以由以下三个要素定义（以8位浮点数为例）：

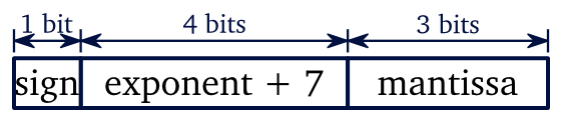
FP8 - (1, 4, 3)

其中，第1位为符号位（0 表示正数，1 表示负数）；中间的 $e=4$ 个比特表示 biased exponent，即 $\mbox{exponent}+(2^{s-1}-1)$（引入bias的目的是在不引入补码的情况下允许负指数，也就是4比特指数的表示范围为 $-7\sim 8$ ）；最后 $m=3$ 个比特表示mantissa的小数部分。以 $5.5_ {(10)}=1.011_ {(2)}\times 2^2$ 为例，将其表示为 FP8-(1,4,3) 的形式，则符号位为 0，四位 biased exponent 为 $2+7=9_ {(10)}=1001_ {(2)}$ ， mantissa 为 $1.011$ 小数点后的三位 $011$ (对于二进制计数法，小数点前面一定是 1，所以可以舍掉以节省空间¹）。相比于定点数，取决于 exponent 的取值，浮点数允许 “.” 在给定存储位的“任何”位置上浮动，由此得名。

FP8-(1,4,3) 可以表示的最大正数为 $1.111_ {(2)}\times 2^{15-7}=111100000_ {(2)}=480_ {(10)}$ ；可以表示的最小正数为 $1.000_ {(2)}\times 2^{0-7}=2^{-7}\approx 0.0078_ {(10)}$ 。相比于（8，4）定点数（不考虑零点，最大可表示正数为 $2^3=8_ {(10)}$ ，最小可表示正数为 $2^{-4}=0.0625_ {(10)}$ ），显然，浮点数可以处理更宽范围内的数。然而，不要忘了，我们始终还是只有8个存储位；换言之，最多也只能表示 $2^8=256$ 个不同的值。下图分别罗列了（8，4）定点数（左图）和 FP8-(1,4,3) 浮点数（右图）所表示的256个数字在数轴上的位置（为清楚展示，做了下采样）：

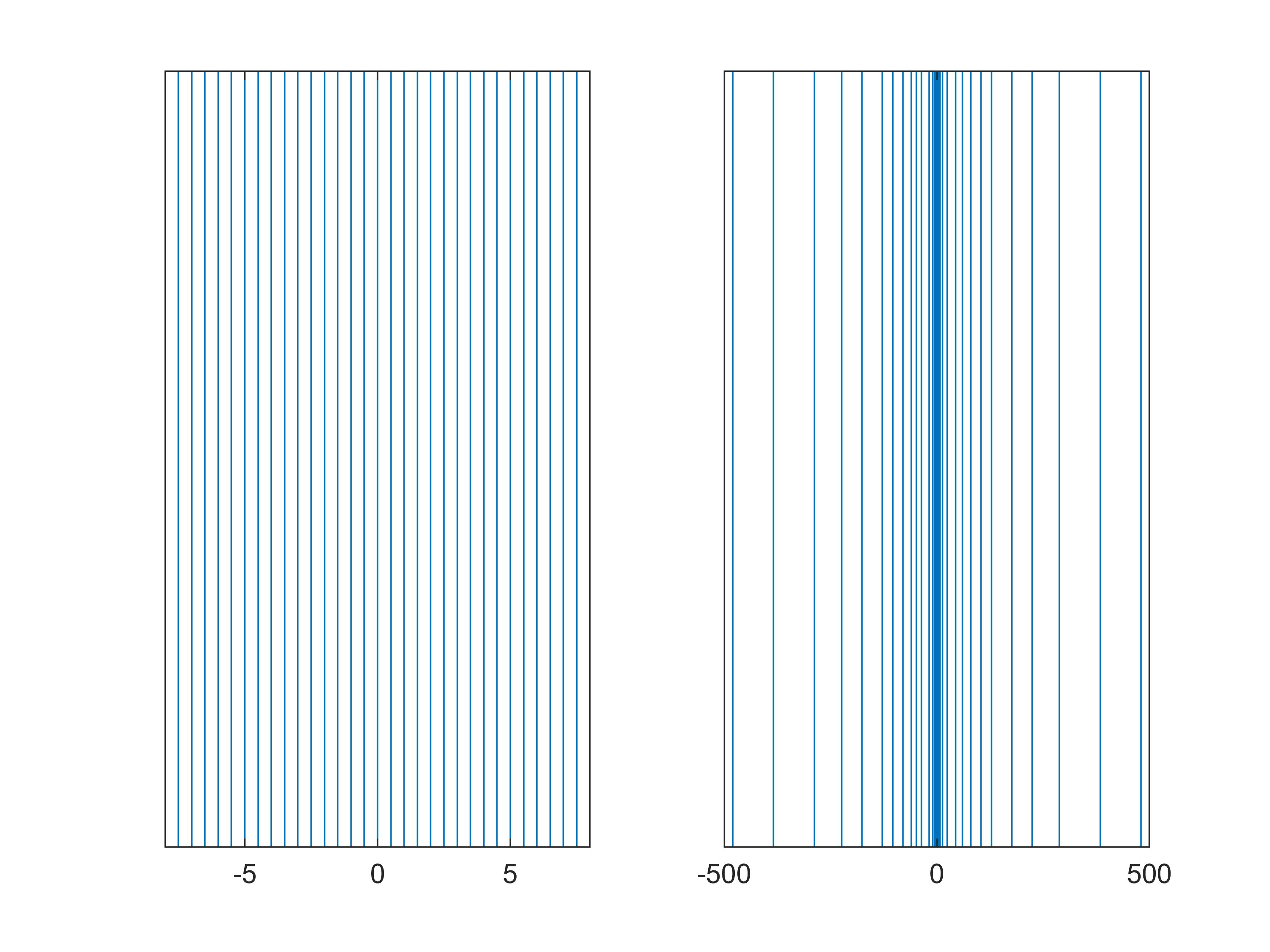
可以注意到，定点数是均匀的，其相邻两数的间隔固定为 $2^{-4}=0.0625$ ；而浮点数却并不是均匀分布的，相反，相邻两数之间的差值随着远离零点越来越大。所以，信息密度的不均匀正是使得浮点数得以处理更大范围的数值的原因。而从工程角度讲，这种不均匀的信息密度也是有道理的——保证相对误差较小。

最后给出将一个十进制实数转换（量化）为浮点数的具体过程（注意，尾数的舍入规则是保证 mantissa 最后一位是0，从而使得一半的数向上取”整“，一半的数向下取”整“）：

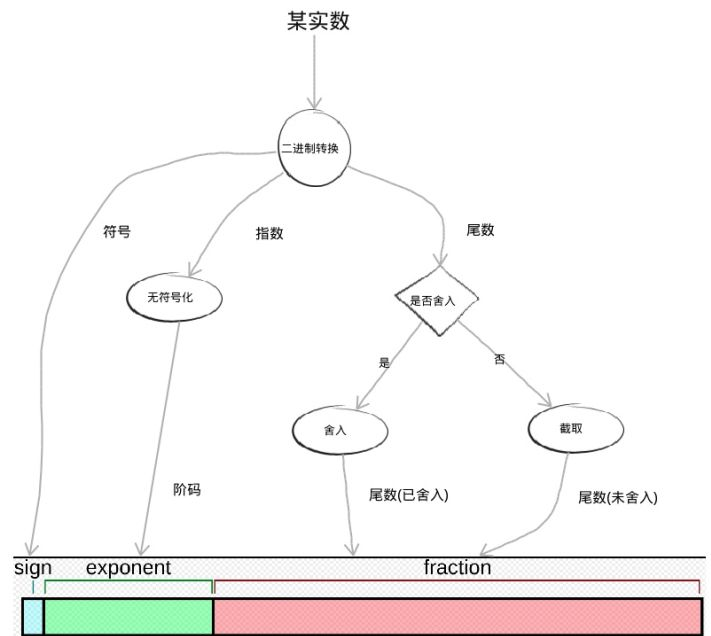
IEEE 754标准

对于给定的存储位数，分配不同的位数给 exponent 和 mantissa，会得到不同的浮点数格式。今天几乎所有的计算机都遵循 IEEE 754 标准（1985年）来表示浮点数，具体格式如下：

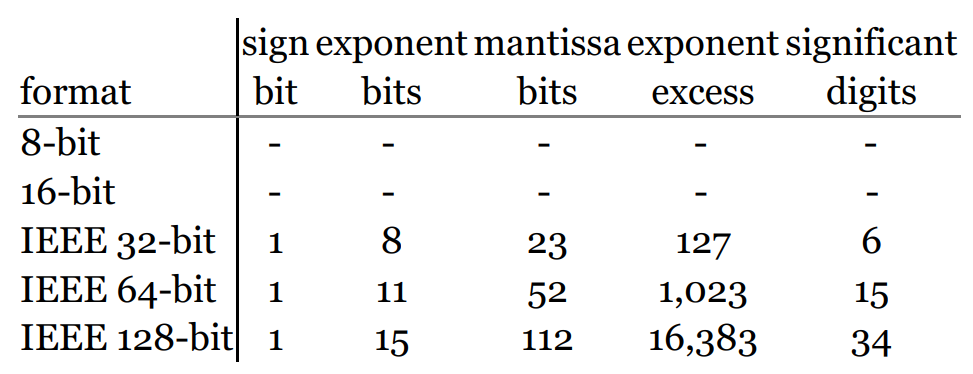
IEEE 只规定了 32 位（single/float）、64 位（double）以及 128 位浮点数的格式，对于更低位的浮点数则并未给出²。标准的基本规则和前节所述一致，此外，标准使用了两种特殊情况来处理非常小和非常大的值。

Denormalized numbers

第一种特殊情况是处理非常小的值。前面说到，为了节省一个存储位，mantissa 部分舍掉了 “.” 前面的 1，导致浮点数无法表示零点。事实上，问题还远不止这些。下图给出了 FP8-(1, 4, 3) 可表示的值在零点附近的分布。

Distribution of small values for (1, 4, 3)-Floating Point (simple)

最小的正数为 $2^{-7}=1/128$（bit pattern $0\;0000\;000$），最大的负数为 ${-}2^{-7}=-1/128$（bit pattern $1\;0000\;000$），二者之间存在一个包括零点在内的巨大 gap！为了解决这个问题，IEEE 754 标准对具有最紧密间隔的那些点（上图中的蓝色空心圆）对应的位模式进行了重新定义，以将它们均匀地分布在缺口范围内，产生下图中的红色空心圆：

Distribution of small values for (1, 4, 3)-Floating Point (IEEE)

为了实现这一点，具体而言，simple 格式中蓝色空心圆对应的位模式的 exponent 位为全 0；对于这样的位模式，IEEE 754 对其含义进行了重新定义：当 exponent 位为全0时，其 exponent 为 $0-(\text{bias}-1)=-6$，mantissa 的 “.” 前面置为 0。以 $0\;0000\;010$为例，在 simple 格式下，其表示数值 $1.010_ {(2)}\times 2^ {-7}$；在 IEEE 格式下，其表示 $0.010_ {(2)}\times 2^ {-6}$。由于其 mantissa 部分不符合科学计数法规则，这些红色空心圆即被称为非规格数³（denormalized numbers）。

Non-numeric values

第二个需要考虑的是处理超出所定义数字范围的计算。IEEE 754 保留了几个特殊的位模式用以表示 $\pm \infty$ 和 NaN (Not a Number)：

• exponent 位全 1、mantissa 位全 0，表示 $\pm\infty$（取决于符号位），解决溢出的问题；
• exponent 位全1、mantissa 具有非 0 位，表示 NaN，用以返回一些错误情况（例如，$0\div 0$）。

对于高位宽浮点数，保留 exponent 位为全1的位模式影响不大；但对于低位宽浮点数，如 FP8 - (1, 4, 3)，总共只有16个 exponent 取值，这样做可能就有些浪费了。所以，在制定低位宽浮点数格式时，处理 non-numeric values 可能需要其它的手段。